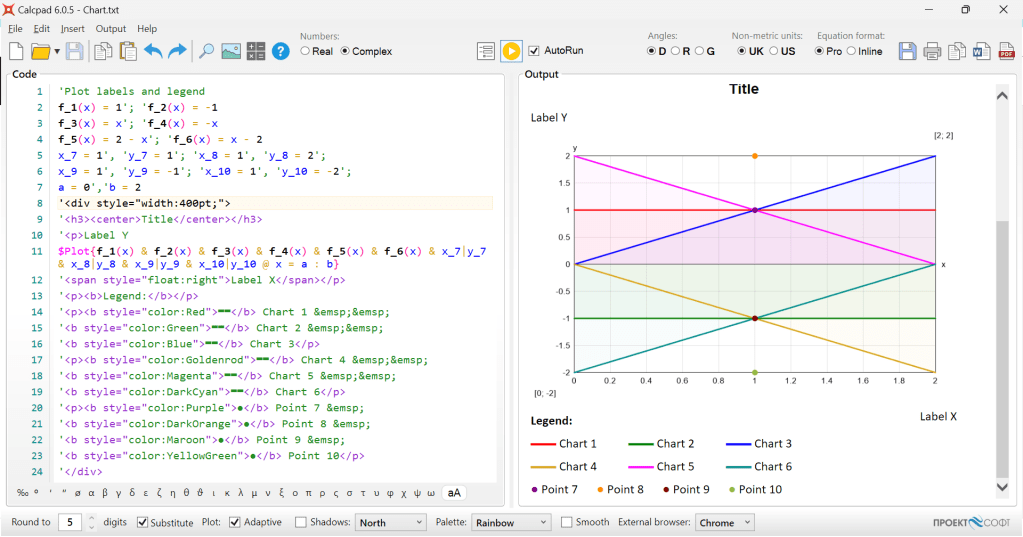
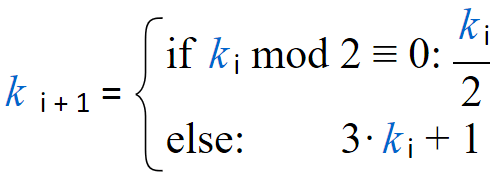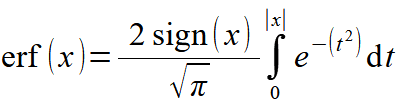Since version 7.3.1, Calcpad supports  Markdown in comments besides simple text and Html/CSS. Markdown is a simple markup language that allows users to quickly format text by adding short symbolic tags. It is easier to use and learn than Html and much faster to type. Although it provides limited features, they are just enough for most of the documents. And there is a good news, if they are not – you can still use Html and CSS if needed because it is finally converted to Html.
Markdown in comments besides simple text and Html/CSS. Markdown is a simple markup language that allows users to quickly format text by adding short symbolic tags. It is easier to use and learn than Html and much faster to type. Although it provides limited features, they are just enough for most of the documents. And there is a good news, if they are not – you can still use Html and CSS if needed because it is finally converted to Html.
Formatting options
Calcpad supports most of the common inline tags but not complicated multiline tags like tables and numbered lists. The reason is that Calcpad parses and executes the code line by line. The available Markdown tags that you can use in Calcpad are listed in the following table:
| Markdown code | Html code | Output |
|---|---|---|
### Heading 3 | <h3>Heading 3</h3> | Heading 3 |
#### Heading 4 | <h4>Heading 4</h4> | Heading 34 |
##### Heading 5 | <h5>Heading 5</h5> | Heading 5 |
###### Heading 6 | <h6>Heading 6</h6> | Heading 6 |
--- (horizontal line) | <hr/> | ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ |
**Bold** | <strong>Bold</strong> | Bold |
*Italic* | <em>Italic</em> | Italic |
***Bold Italic*** | <em><strong>Bold Italic</strong></em> | Bold Italic |
++Underlined++ | <ins>Underlined</ins> | Underlined |
~~Struck through~~ | <del>Struck through</del> | |
==Highlighted== | <mark>Highlighted</mark> | Highlighted |
x^superscript^ | x<sup>superscript</sup> | xsuperscript |
x~subscript~ | x<sub>subscript</sub> | xsubscript |
`Code` | <code>Code</code> | Code |
[Link](https://mywebsite.com) | <a href=”https://mywebsite.com”>Link</a> | Link |
 | <img src=”image.jpg” alt=”Image” /> |  |
> Blockquote 1 | <blockquote>Blockquote 1 <blockquote>Blockquote 2</blockquote></blockquote> | Blockquote 1 Blockquote 2 |
How to use Markdown in Calcpad
Markdown is not enabled in Calcpad by default. In order to get your markup recognized in your worksheet, you have to turn Markdown on by adding the following line above:
#md onAnd if you want to turn it off, simply write:
#md offMarkdown tags should be used only inside text comments, enclosed by ‘quotes’. Everything outside quotes is treated as math expressions. You can find an example about using Markdown in Calcpad on GitHub:
https://github.com/Proektsoftbg/Calcpad/blob/main/Examples/Demos/Markdown.cpd

You can type the tags manually, or you can use the formatting toolbar above the code window. Just switch the  button on the right hand side on. Otherwise, the buttons will insert Html even if you have set
button on the right hand side on. Otherwise, the buttons will insert Html even if you have set #md on in your code.

Calculation notes with Markdown
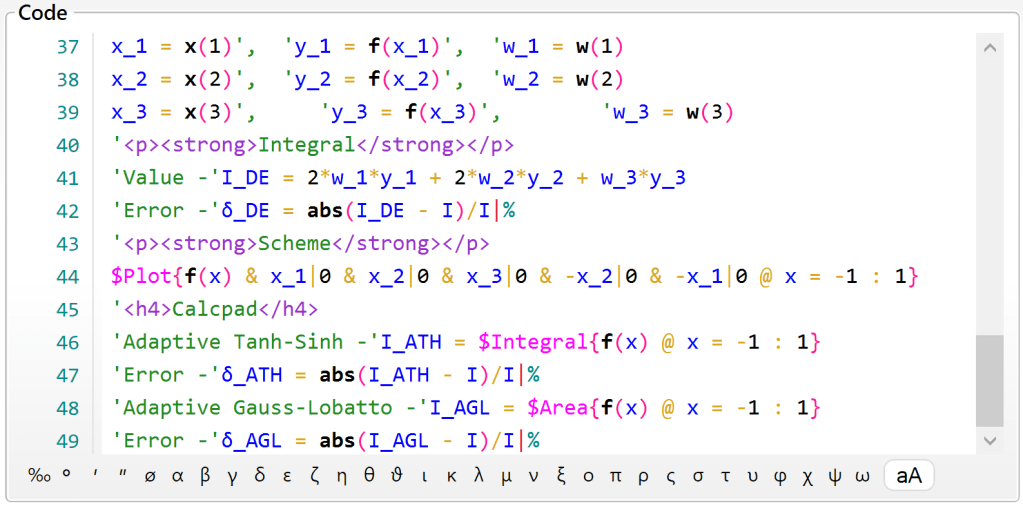
By mixing Markdown with equations in Calcpad, you can create professionally formatted reports for your engineering calculations and export them to Html, Pdf and MS Word files. To demonstrate this, we created a sample RC beam design worksheet to Eurocode 2:
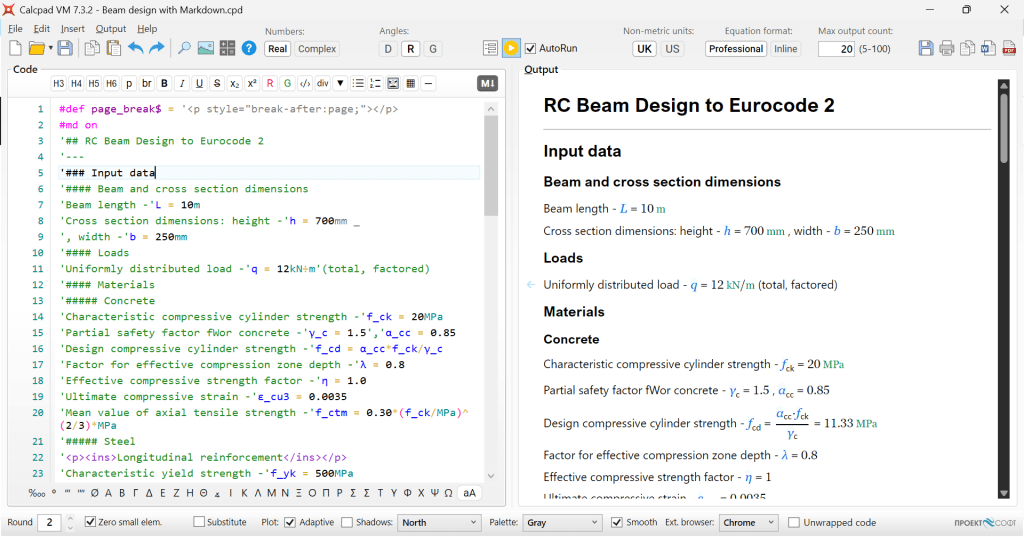
Source code
#def page_break$ = '<p style="break-after:page;"></p>
#md on
'## RC Beam Design to Eurocode 2
'---
'### Input data
'#### Beam and cross section dimensions
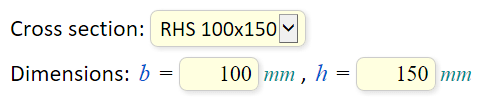
'Beam length -'L = 10m
'Cross section dimensions: height -'h = 700mm _
', width -'b = 250mm
'#### Loads
'Uniformly distributed load -'q = 12kN÷m'(total, factored)
'#### Materials
'##### Concrete
'Characteristic compressive cylinder strength -'f_ck = 20MPa
'Partial safety factor fWor concrete -'γ_c = 1.5','α_cc = 0.85
'Design compressive cylinder strength -'f_cd = α_cc*f_ck/γ_c
'Factor for effective compression zone depth -'λ = 0.8
'Effective compressive strength factor -'η = 1.0
'Ultimate compressive strain -'ε_cu3 = 0.0035
'Mean value of axial tensile strength -'f_ctm = 0.30*(f_ck/MPa)^(2/3)*MPa
'##### Steel
'<p><ins>Longitudinal reinforcement</ins></p>
'Characteristic yield strength -'f_yk = 500MPa
'Partial safety factor for steel -'γ_s = 1.15
'Design yield strength -'f_yd = f_yk/γ_s
'Modulus of elasticity -'E_s = 200000MPa
page_break$
'++Shear reinforcement++
'Characteristic yield strength -'f_ywk = 500MPa
'Design yield strength -'f_ywd = f_yk/γ_s
'### Results
'#### Internal forces
'Support reaction -'A = q*L/2
'Shear force diagram -'V(x) = A - q*x
'<!--'PlotHeight = 100'-->
$Plot{V(x) @ x = 0m : L}
'Design shear force -'V_Ed = A
'Bending moment diagram -'M(x) = A*x - q*x^2/2
$Plot{M(x) @ x = 0m : L}
'Design bending moment -'M_Ed = q*L^2/8
page_break$
'### Bending design
'Concrete cover to the center of reinforcement -'d_1 = 50mm
'Effective cross section depth -'d = h - d_1'cm
'Relative design bending moment -'m_Ed = M_Ed/(b*d^2*η*f_cd)
'Compressive zone depth -'x = d/λ*(1 - sqr(1 - 2*m_Ed))
'Relative compression zone depth -'ξ = x/d
'Design reinforcement yield strain -'ε_yd = f_yd/E_s
'Relative depth of compression zone at yielding of bottom reinforcement
ξ_yd = ε_cu3/(ε_cu3 + ε_yd)
'Limit compression zone depth -'ξ_lim = ξ_yd
'(*ξ*~lim~ = *ξ*~yd~ for elastic and *ξ*~lim~ = 0.45 for plastic analysis)
ξ'≤'ξ_lim'- Compressive reinforcement is **NOT** required.
'Lever arm of internal forces -'z = d - 0.5*λ*x
'Required main reinforcement -'A_sL,rq = M_Ed/(z*f_yd)|mm^2
'Selected'n_b = 3'bars with size'Ø_L = 20mm
'Provided main reinforcement'A_sL = n_b*π*Ø_L^2/4
'Reinforcement ratio -'ρ_L = A_sL/(b*d)
'Minimum reinforcement ratio
ρ_min = max(0.26*f_ctm/f_yk; 0.0013)'<'ρ_L
'Maximum reinforcement ratio -'ρ_max = 0.04'>'ρ_L
page_break$
'### Shear design
'Shear capacity without reinforcement
k = min(1 + sqr(200mm/d); 2)', 'C_Rd_c = 0.18/γ_c', 'k_1 = 0.15', 'σ_cp = 0MPa
v_min = 0.035*k^(3/2)*sqr(f_ck/MPa)*MPa
V_Rd_c_ = (C_Rd_c*k*(100*ρ_L*f_ck/MPa)^(1/3)*MPa + k_1*σ_cp)*b*d
'Minimum shear resistance
V_Rd_c_min = (v_min + k_1*σ_cp)*b*d
V_Rd_c = max(V_Rd_c_min; V_Rd_c_)
'Design check:
V_Ed'≤'V_Rd_c'. Shear reinforcement is **NOT** required by calculations!
'Nominal reinforcement will be provided as follows:
'Shear links with'n_w = 2'legs and diameter -'d_w = 6mm
'Area of one leg -'A_sw1 = π*(d_w/2)^2
'Maximum stirrup spacing -'s_max = min(0.75*d; 300mm)
'Provided stirrup spacing -'s = s_max
'Provided shear reinforcement area -'A_sw = n_w*A_sw1*(1m/s)'/m
'Reinforcement ratio -'ρ_w = A_sw/(s*b)
ρ_w_min = 0.08*sqr(f_ck/MPa)*MPa/f_yk'<'ρ_wReport
Disclaimer:
The example does not cover all aspects of beam design and all possible cases. It is created with the sole purpose to demonstrate how to compose and format an engineering calculation worksheet with Markdown.