Checking the Collatz conjecture (with Calcpad)

The Collatz conjecture is one of the most interesting and still unsolved problems in mathematics. It is named after the German mathematician Lothar Collatz (1910 – 1990), who invented it. It sounds very simple, and it is hard to believe that no one has managed to prove it so far:

Pick a random integer > 1. It it is even, divide by 2. If it is odd, multiply by 3 and add 1. Do the same with the newly calculated value and so on. This is equivalent to the following series:

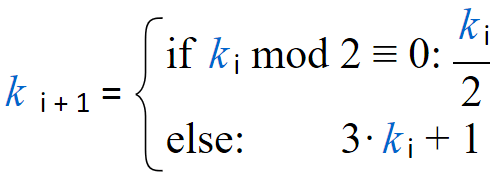
Collatz stated that whatever starting integer k₀ > 1 you take, you will end up with calculating 1. Some curious people have tried this for all integers up to 10²⁰ (at least) by using computers. So far, they haven’t found a single number that contradicted the conjecture.

But in math, this does not prove anything. It is still possible that some larger number exists, that will fail to comply. It may get trapped into an infinite cycle or simply diverge to infinity. So, it works like magic and no one in the world knows exactly why. A detailed explanation of the problem is provided in this YouTube video:

Actually, it is much easier to disprove the Collatz conjecture than proving it. It is enough to find just one number that contradicts the conjecture, and we are ready. No one managed to do that till now, but it doesn’t mean that we cannot try as well. It is quite unlikely to succeed because most probably the conjecture is true. But lets give it a try and hope to be lucky ;).

For that purpose, we will create a short program in Calcpad. Here is the code:

CollatzCheck(k; n) = $Repeat{k = switch(k ≡ 1; 1; k⦼2 ≡ 0; k/2; 3*k + 1) @ i = 1 : n}

That is all we need to do the job – one line of code. Here, k is the starting number and n is the maximum number of steps. According to the data from previous experiments, n is not expected to be larger than 10000. If we fail with this value we can try with a greater one. We can use the above function as follows:

CollatzCheck(100000000000001; 10000)

In return, we get 1 as expected. However, this function does not provide information about the number of steps required to finish (the stopping time). For that purpose, we will use a little hack and modify the function slightly. We will make it to divide by zero when we reach k = 1. This will force it to exit with error and report the value of i:

CollatzSteps(k; n) = $Repeat{k = switch(k ≡ 1; -1/0; k⦼2 ≡ 0; k/2; 3*k + 1) @ i = 1 : n}

After we call the new function:

CollatzSteps(100000000000001; 10000)

we get the following message:

Error in “CollatzSteps(100000000000001; 10000)” on line [ ]: The function k = switch(k ≡ 1; -1/0; k⦼2 ≡ 0; k/2; 3*k + 1) is not defined for i = 252.

Now we know that it needed 252 steps to complete. However, this is not a nice way to return a result. But counting the number of steps and showing better output at the same time already require loops, as follows:

#def Collatz_Check$(k$; n$)
    #hide
    i = 0
    k_ = k$
    #repeat n$
        i = i + 1
        #if k_ ≡ 1
            #break
        #else if k_⦼2 ≡ 0
            k_ = k_/2
        #else 
            k_ = 3*k_ + 1
        #end if
    #loop
    #show
    #val
    #if k_ ≡ 1
        'Collatz check for <b>'k$'</b> <span class="ok">succeeded</span> after 'i' steps.
    #else
        'Collatz check for <b>'k$'</b> <span class="err">failed</span> after 'n$' steps.
    #end if
    #equ
#end def

This time we implemented a macro procedure to organize our code. We can use it for our purposes in the following way:

Collatz_Check$(100000000000001; 1000)

And here is the output:

Collatz check for 100000000000001 succeeded after 252 steps.

There is another improvement that we can apply. With a little modification, we can make the above procedure not only to count the steps, but also to plot them in the output:

#def Collatz_Plot$(k$; n$)
    #hide
    i = 0
    k_ = k$
    #show
    #val
    'Collatz check for <b>'k$'</b>:
    '<table>
    '<tr><td>Start -</td><td>&emsp;'k_'</td></tr>
    #repeat n$
        #hide
        i = i + 1
        #show
        #if k_ ≡ 1
            #break
        #else if k_⦼2 ≡ 0
            '<tr><td>/2 =</td><td>&emsp;'k_ = k_/2'</td></tr>
        #else 
            '<tr><td>*3 + 1 =</td><td>&emsp;'k_ = 3*k_ + 1'</td></tr>
        #end if
    #loop
    '</table>
    #if k_ ≡ 1
        'Check <span class="ok">succeeded</span> after 'i' steps.
    #else
        'Check <span class="err">failed</span> after 'n$' steps.
    #end if
    #equ
#end def

To make the output shorter and save some scrolling, we will use a smaller number to demonstrate this procedure:

Collatz_Plot$(11; 1000)

And this is what we obtain in return:

This is very useful to see how this sequence actually works. First, the expression 3*k + 1 transforms the odd number to even, that will be immediately halved (at least once). Second, if the latest is a multiple of 2ⁿ, we will have n consecutive downsteps, that may go much lower than the initial value. So, maybe we should ask the question: what is the distribution of n for all 2ⁿ multiples in a certain range and now often we will hit a multiple with larger n…

However, if we want to check more numbers, it would be tedious to do it one by one. We should write another procedure that checks all integers in a given range:

#def Collatz_Check_Between$(k0$; kn$; n$)
    #hide
    k0 = max(k0$; 1)
    i = k0 - 1
    #repeat kn$ - k0 + 1
        i = i + 1
        k_ = CollatzCheck(i; n$)
        #if k_ ≠ 1
            #break
        #end if
    #loop
    #show
    #val
    #if k_ ≡ 1
        'Collatz check <span class="ok">succeeded</span> for all numbers between 'k0' and 'kn$'.
    #else
        'Collatz check <span class="err">failed</span> for <b>'i'</b> and 'n$' steps.
    #end if
    #equ
#end def

The above function can be used as given bellow:

Collatz_Check_Between$(2; 100000; 400)

After less than a second we get the result:

Collatz check succeeded for all numbers between 2 and 100000.

So, this is how we can use Calcpad to experiment with the Collatz conjecture. You can download the complete source code for the above examples from GitHub:

https://github.com/Proektsoftbg/Calcpad/blob/main/Examples/Mathematics/Collatz%20Check.cpd

If you still do not have Calcpad, you can download and install it for free from the following link:

https://calcpad.eu/download/calcpad-setup-en-x64.zip

Now you can use Calcpad to perform your own experiments. If you get lucky to disprove the Collatz conjecture, please share credits ;).

If you want to learn more about this spiky mathematical problem, there are various sources in the internet, you can start with:

https://en.wikipedia.org/wiki/Collatz_conjecture

https://mathworld.wolfram.com/CollatzProblem.html